Interface vs Data Structure
| Interface |
Data Structure |
| specification |
representation |
| what data can store |
how to store data |
| what operations are supported |
algorithms to support operations |
| problem |
solution |
Two main interfaces
- Sequence Interface
- Set Interface
Sequence Interface
- Sequences maintain a collection of items in an extrinsic order, where each item stored has a rank in the sequence, including a first item and a last item.
- By extrinsic, we mean that the first item is ‘first’, not because of what the item is, but because some external party put it there.
- Sequences are generalizations of stacks and queues, which support a subset of sequence operations.
|
Operation |
Description |
| Container(general type) |
build(X) |
given an iterable X, build sequence from items in X |
| len() |
return the number of stored items |
| Static(the number of items doesn’t change) |
iter_seq() |
return the stored items one-by-one in sequence order |
| get_at(i) |
return the ith item |
| set_at(i, x) |
replace the ith item with x |
| Dynamic(the number of items can be change) |
insert_at(i, x) |
add x as the ith item |
| delete_at(i) |
remove and return the ith item |
| insert first(x) |
add x as the first item |
| delete first() |
remove and return the first item |
| insert last(x) |
add x as the last item |
| delete last() |
remove and return the last item |
(Note that insert / delete operations change the rank of all items after the modified item.)
Array Sequence
- A fixed-length array is the data structure.
Linked List Sequence
- A linked list stores each item in a node, node, a constant-sized container with two properties: node.item storing the item, and node.next storing the memory address of the node containing the next item in the sequence.
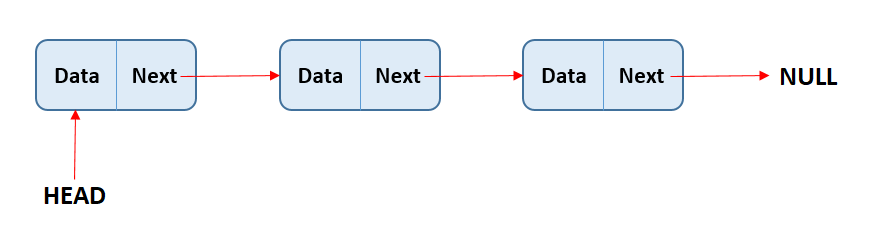
(Source: habr)
Dynamic Array Sequence
- Like array, but this size is variable.
Summary
|
build(X) |
get_at(i), set_at(i) |
insert_first(x), delete_first() |
insert_last(x), delete last() |
insert_at(i, x), delete at(i) |
| Array |
O(n) |
O(1) |
O(n) |
O(n) |
O(n) |
| Linked List |
O(n) |
O(n) |
O(1) |
O(n) |
O(n) |
| Dynamic Array |
O(n) |
O(1) |
O(n) |
O(1) |
O(n) |
Set Interface
- Storing items in an array in arbitrary order can implement a (not so efficient) set
|
Operation |
Description |
| Container |
build(X) |
given an iterable X, build set from items in X |
| len() |
return the number of stored items |
| Static |
find(k) |
return the stored item with key k |
| Dynamic |
insert(x) |
add x to set (replace item with key x.key if one already exists) |
| delete(k) |
remove and return the stored item with key k |
| Order |
iter ord() |
return the stored items one-by-one in key order |
| find min() |
return the stored item with smallest key |
| find max() |
return the stored item with largest key |
| find next(k) |
return the stored item with smallest key larger than k |
| find prev(k) |
return the stored item with largest key smaller than k |
留言
張貼留言